Définition
A et B sont deux événements d’une expérience aléatoire.
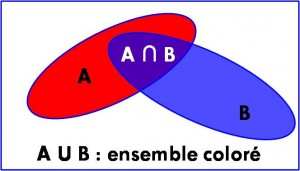
=> L’intersection des événements, notée A ∩ B, est l’ensemble des résultats qui réalisent à la fois les deux événements A et B.
=> La réunion des événements, notée A ∪ B, est l’ensemble des résultats qui réalisent l’un ou l’autre des événements A et B.
=> La probabilité de la réunion des événements A et B se calcule par la relation :
p(A∪B) = p(A) + p(B) – p(A∩B).
=> L’intersection des événements, notée A ∩ B, est l’ensemble des résultats qui réalisent à la fois les deux événements A et B.
=> La réunion des événements, notée A ∪ B, est l’ensemble des résultats qui réalisent l’un ou l’autre des événements A et B.
=> La probabilité de la réunion des événements A et B se calcule par la relation :
p(A∪B) = p(A) + p(B) – p(A∩B).

Exemple :
La classe de terminale GA participe à la journée sportive de solidarité Bouge Ton Coeur. On interroge les élèves sur leur participation :
Sur 20 filles 12 participent dans une équipe, sur 10 garçons il n’y a que 40% qui participent ans un équipe.
Sur 20 filles 12 participent dans une équipe, sur 10 garçons il n’y a que 40% qui participent ans un équipe.
1. Compléter le tableau suivant :
| Elèves | Joueurs | Spectateurs | TOTAL |
| Garçons | …….. | …….. | …….. |
| Filles | …….. | …….. | …….. |
| TOTAL | …….. | …….. | …….. |
| Elèves | Joueurs | Spectateurs | TOTAL |
| Garçons | 4 | 6 | 10 |
| Filles | 12 | 8 | 20 |
| TOTAL | 16 | 14 | 30 |
2. Calculer la probabilité de l’évènement A « l’élève interrogé est une fille ».
p(A)=\dfrac{20}{30}= 0,67
3. Calculer la probabilité de l’évènement B « l’élève interrogé est un joueur ».
p(B)=\dfrac{16}{30}= 0,53
4. Cocher la bonne notation de l’évènement C « l’élève interrogé est une fille joueuse dans une équipe ».
\quad \Box A U B \quad \Box A ∩ B \quad \Box A x B
\quad \Box A U B \quad \Box A ∩ B \quad \Box A x B
\quad \Box A U B \quad \boxtimes A ∩ B \quad \Box A x B
5. Calculer la probabilité de l’évènement C « l’élève interrogé est une fille joueuse dans une équipe ».
p(B)=\dfrac{12}{30}= 0,4
6. Cocher la bonne notation de l’évènement D « l’élève interrogé est une fille ou un(e) joueur(se) dans une équipe ».
\quad \Box A U B \quad \Box A x B \quad \Box A ∩ B
\quad \Box A U B \quad \Box A x B \quad \Box A ∩ B
\boxtimes A U B \quad \Box A ∩ B \quad \Box A x B
7. Calculer la probabilité de l’évènement D « l’élève interrogé est une fille ou un(e) joueur(se) dans une équipe ».
p(A U B) = p(A) + p(B) – p(A ∩ B)
p(D) = p(A) + p(B) – p(C) = 0,67 + 0,53 – 0,40 = 0,80
Autre Méthode :
Le nombre d’élèves concernés par l’évènement D est : 20 filles + 4 garçons joueurs = 24 élèves
p(D)=\dfrac{24}{30}= 0,80
p(D) = p(A) + p(B) – p(C) = 0,67 + 0,53 – 0,40 = 0,80
Autre Méthode :
Le nombre d’élèves concernés par l’évènement D est : 20 filles + 4 garçons joueurs = 24 élèves
p(D)=\dfrac{24}{30}= 0,80