Définition
Un arbre des évènements est un schéma permettant de déterminer toutes les issues possibles lors d’une succession d’expériences aléatoires.
A chaque étape il faut notifier une issue possible par une ramification.
La somme des probabilités de chaque étape est égale à 1.
A chaque étape il faut notifier une issue possible par une ramification.
La somme des probabilités de chaque étape est égale à 1.
Exemple
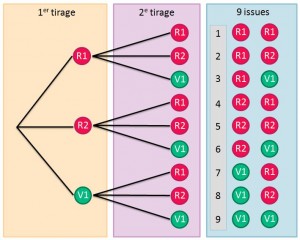
Une urne contient 2 boules rouges et 1 boule Verte.
On réalise deux tirages successifs avec remise.
Voici l’arbre des évènements représentant cette expérience.
On réalise deux tirages successifs avec remise.
Voici l’arbre des évènements représentant cette expérience.

Application
Une urne contient 2 boules rouges, 3 boules Bleues et 4 boules Vertes.
On réalise trois tirages successifs sans remise.
On réalise trois tirages successifs sans remise.
1. Combien de possibilités avons-nous au premier tirage ?
Au premier tirage on a 3 possibilités correspondant à chacune des couleurs Rouge, Bleu et Vert.
2. Combien de possibilités avons-nous au deuxième tirage ?
Au deuxième tirage il existe encore des boules de chacune des trois couleurs, on a 3 possibilités correspondant à chacune des couleurs Rouge, Bleu et Vert.
3. Combien de possibilités avons-nous au troisième tirage ?
Si une boule rouge a été tirée à chaque fois des deux premiers tirages, il n’y a plus de boules rouges dans l’urne. Donc ce cas il ne reste plus que deux possibilités : bleu et Vert.
Sinon il reste toujours 3 possibilités car il existe encore des boules des trois couleurs.
Sinon il reste toujours 3 possibilités car il existe encore des boules des trois couleurs.
4. Réaliser un arbre des évènements correspondant à cette expérience.
5. Combien existe-t-il d’issues possibles au total ?
On a 26 issues possibles.
Soit l’évènement A « Obtenir trois boules de couleurs différentes ».
6. Combien existe-t-il d’issues favorables à l’évènement A ?
On a 6 issues favorables.
7. Quelle est la probabilité de l’évènement A ?
p(A)=\dfrac{6}{26}= 0,231
Soit l’évènement B « Obtenir au moins deux boules de couleurs identiques ».
8. Combien existe-t-il d’issues favorables à l’évènement B ?
On a 20 issues favorables.
9. Quelle est la probabilité de l’évènement B ?
p(A)=\dfrac{20}{26}= 0,769