L’entreprise C.S.I.I. produit des articles du domaine informatique pour l’Europe.
Le coût de production C(n) exprimé en milliers d’euro pour n articles est donné par la fonction C avec : C(n)=0,02n^2-2n+98 pour n appartenant à l’intervalle [50 ; 150].
Le montant des ventes V(n) exprimé en milliers d’euro est pour sa part donné par la fonction V avec V(n)=1,5n pour n appartenant à l’intervalle [50 ; 150].

1. Compléter le tableau suivant :

n	50	60	75	90	100	125	150
C(n)	…	50	…	…	98	…	248

2. Tracer dans le même repère à l’aide de Géogébra les courbes représentant les fonctions C et V.

3. Déterminer graphiquement l’intervalle des valuers de n pour lesquelles la production est rentable.

4. Le bénéfice B(n) est donné par la fonction B pour n appartenant à l’intervalle [50 ; 150].
Exprimer B(n) en fonction de n et déterminer la dérivée B'(n).

5. En déduire le nombre d’articles à vendre pour que le bénéfice soit maximum.

Pour contrer l’offensive du commerce sur Internet dans le domaine de la cosmétique, le salon SANTÉ-BEAUTÉ a investi, depuis 4 ans, dans la publicité et l’aménagement de son point de vente. Le responsable du salon a constaté que pour une somme investie s (exprimée en k€), le résultat R réalisé, vérifie la formule R(s)=-6s^2+60s+12 pour

1.Calculer le résultat pour une somme investie de 3 k€.

Soit la fonction f définie sur l’intervalle [1,5;6] par : f(x)=-6x^2+60x+12

2.a. Soit f' la fonction dérivée de la fonction f sur l’intervalle [1,5;6]. Calculer f'(x).

2.b. Résoudre l’équation f'(x)=0.

2.c. Compléter le tableau de variation de la fonction f.

x
f'(x)
f(x)

2.d. En utilisant le logiciel Géogébra, représenter graphiquement la fonction f.

2.e. Donner le maximum de la fonction f sur [1,5 ; 6].

3. En utilisant les réponses précédentes, donner le montant de l’investissement (en euros) qui permet d’obtenir un résultat maximum.

Après avoir transformé ses magasins, une chaîne s’intéresse au lancement d’une nouvelle ligne de produits biologiques sur le marché.
Pour faire connaitre ces produits, les dirigeants décident de créer une pochette « découverte » qui sera proposée au prix de 2 €.
On étudie la rentabilité de cette opération sur une journée sachant qu’au maximum 400 pochettes peuvent être fabriquées chaque jour.

1) Calculer la recette réalisée dans le cas de :
a) 100 pochettes vendues par jour.
b) 400 pochettes vendues par jour.

2) On note R la recette journalière et n le nombre de pochettes vendues par jour.
Exprimer R(n) en fonction de n.

3. Le coût de fabrication journalier, en euros, de cette pochette est modélisé par la fonction f
définie sur l’intervalle [0;400] telle que f(x)=-0,01x^2+5x+10.

a. Déterminer f'(x).

b. Résoudre l’inéquation f'(x)>0.

c. Compléter le tableau de variations.

4. A l’aide de Géogébra, tracer dans le repère suivant les représentations graphique de f(x)=-0,01x^2+5x+10 et y=2x sur l’intervalle [0;400] puis le point d’intersection de ces représentations graphiques.

5. Donner, en justifiant votre réponse, le nombre minimum de pochettes qu’il est nécessaire de vendre pour que l’opération soit rentable.

On considère la fonction f définie sur l’intervalle I=[18;40] par : f(x)=-1,5x^2+84x-950

1) Calculer f'(x) où f' désigne la dérivée de la fonction f.
2) Étudier le signe de f'(x) sur l’intervalle I=[18;40].
3) Établir le tableau de variations de la fonction f sur l’intervalle I=[18;40].
4) En déduire la valeur de x pour laquelle la fonction f admet un maximum.

Dans une grande surface, un samedi, le nombre de clients N(t) présents dans le magasin en fonction de l’heure t est donné par :
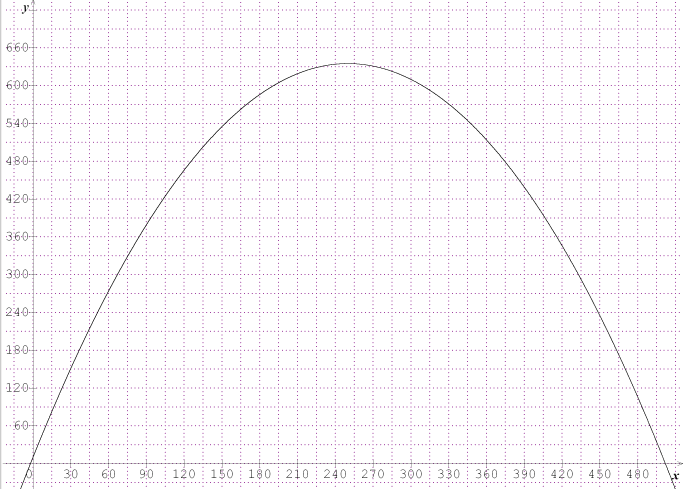
N(t)=-5t^3+225t^2-3240t+15250 Les heures sont dans l’intervalle I=[10;20]
1) Compléter le tableau de valeurs de la fonction N situé ci-dessous.

t	10	11	12	13	14	15	16	17	18	19	20
N(t)	350					400					450

2) Placer les points correspondants dans le repère situé ci-après. Tracer la courbe représentative de la fonction N sur l’intervalle I=[10;20].

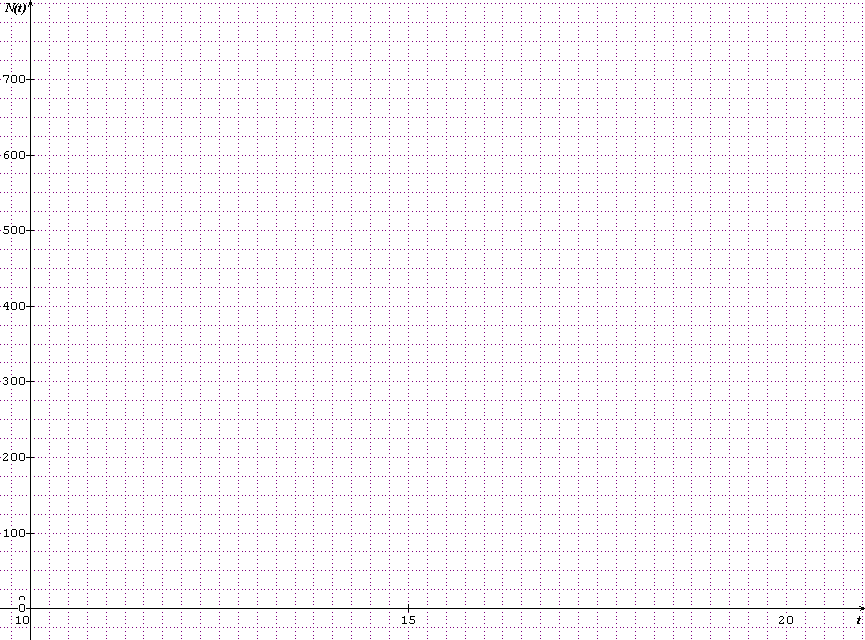
3) Déterminer graphiquement le nombre de clients présents à 15 heures 30 minutes. Laisser apparents les traits permettant la lecture graphique.
4) Soit N' la fonction dérivée de N. Déterminer N'(t).
5) Vérifier que N'(t)=0 équivaut à t^2-30t+216=0.
6) Résoudre cette équation.
7) Compléter le tableau de variation situé ci-dessous.

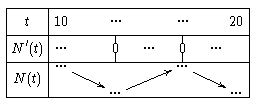
8) Déduire des résultats précédents l’heure à laquelle il faut prévoir un maximum de caissières pour fluidifier le passage aux caisses.