Archives de catégorie : Terminale
FD10 – Troisième problème
Le coût de production C(n) exprimé en milliers d’euro pour n articles est donné par la fonction C avec : C(n)=0,02n^2-2n+98 pour n appartenant à l’intervalle [50 ; 150].
Le montant des ventes V(n) exprimé en milliers d’euro est pour sa part donné par la fonction V avec V(n)=1,5n pour n appartenant à l’intervalle [50 ; 150].
| n | 50 | 60 | 75 | 90 | 100 | 125 | 150 |
| C(n) | … | 50 | … | … | 98 | … | 248 |
C(75)=60,5
C(90)=80
C(125)=160,5
Exprimer B(n) en fonction de n et déterminer la dérivée B'(n).
B(n)==1,5n-(0,02n^2-2n+98)
B(n)=-0,02n^2+3,5n-98
B'(n)=-0,04n+3,5
-0,04n+3,5=0
-0,04n=-3,5
n=87,5
Le nombre d’article est maximum pour n=87,5 car la fonction B est une fonction carrée et sa dérivée change de signe en n=87,5.
FD09 – Deuxième problème
R(s)=138
-12x=-60
x=\dfrac{-60}{-12}
x=5
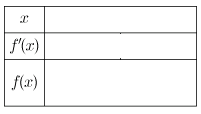
| x | |
| f'(x) | |
| f(x) |
f(5)=162
FD08 – Premier problème
Pour faire connaitre ces produits, les dirigeants décident de créer une pochette « découverte » qui sera proposée au prix de 2 €.
On étudie la rentabilité de cette opération sur une journée sachant qu’au maximum 400 pochettes peuvent être fabriquées chaque jour.
a) 100 pochettes vendues par jour.
b) 400 pochettes vendues par jour.
a) 100 pochettes : 100 \times 2=200
b) 400 pochettes : 400 \times 2=800
Exprimer R(n) en fonction de n.
définie sur l’intervalle [0;400] telle que f(x)=-0,01x^2+5x+10.
donc -0,02x>-5
donc x<\dfrac{5}{0,02} ou x<250 soit I=[0;250[
FD07 – Premier exercice complet et problème
1) Calculer f'(x) où f' désigne la dérivée de la fonction f.
2) Étudier le signe de f'(x) sur l’intervalle I=[18;40].
3) Établir le tableau de variations de la fonction f sur l’intervalle I=[18;40].
4) En déduire la valeur de x pour laquelle la fonction f admet un maximum.
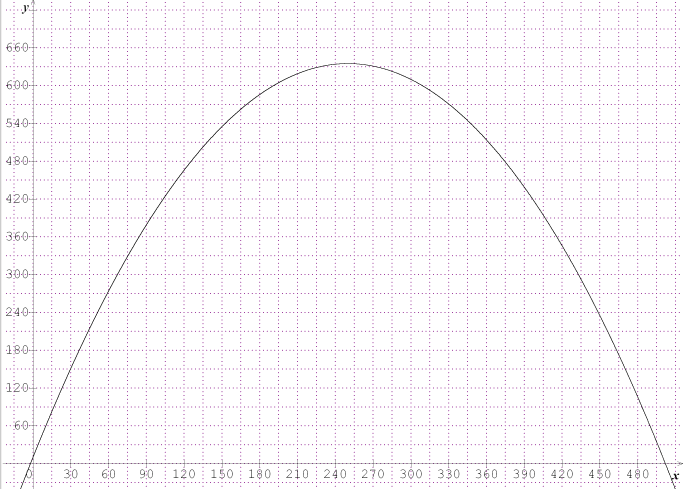
N(t)=-5t^3+225t^2-3240t+15250 Les heures sont dans l’intervalle I=[10;20]
1) Compléter le tableau de valeurs de la fonction N situé ci-dessous.
| t | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| N(t) | 350 | 400 | 450 |
2) Placer les points correspondants dans le repère situé ci-après. Tracer la courbe représentative de la fonction N sur l’intervalle I=[10;20].
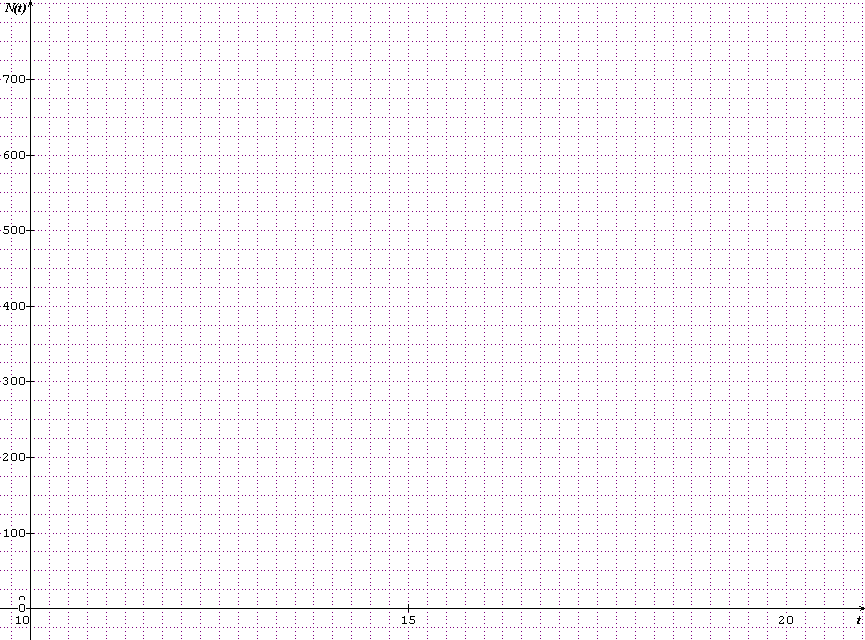
3) Déterminer graphiquement le nombre de clients présents à 15 heures 30 minutes. Laisser apparents les traits permettant la lecture graphique.
4) Soit N' la fonction dérivée de N. Déterminer N'(t).
5) Vérifier que N'(t)=0 équivaut à t^2-30t+216=0.
6) Résoudre cette équation.
7) Compléter le tableau de variation situé ci-dessous.
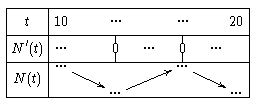
8) Déduire des résultats précédents l’heure à laquelle il faut prévoir un maximum de caissières pour fluidifier le passage aux caisses.
FD06 – Tableau de variation
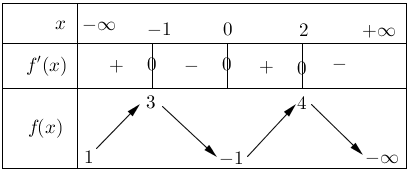
① Ce tableau se base sur l’ensemble de définition I de la fonction qui vous sera donné.
Dans ce tableau de variation doit figurer les abscisses de I ainsi que les valeurs particulières qui annulent la dérivée.
| x | -\infty | -1 | 0 | 2 | +\infty |
﹖⃝Ici l’ensemble de définition est ]-\infty;+\infty[ avec 3 valeurs particulières -1;0;2.
—————–
② On doit y trouver aussi une étude du signe de la dérivée.
| f'(x) | + | 0 | - | 0 | + |
﹖⃝Ici le signe de la dérivée change aux valeurs particulières -1;0;2.
—————–
③ Et enfin les variations de la fonction symbolisées par des flèches.
On en conclut les variations de la fonctions avec des flèches montantes pour de la croissance, descendante pour de la décroissance et horizontale pour la constance.
⚠ N’oubliez d’inscrire les valeurs des images des valeurs particulières par la fonction f.
① On calcule la dérivée de la fonction f : f'(x)=6x+12
② On résout l’équation f'(x)=0 : 6x+12=0 ou x=-2
La dérivée s’annule donc en -2, la fonction change de signe en ce point.
③ On étudie le signe de la dérivée de f :
f'(x)>0 quand x>-2
f'(x)<0 quand x<-2 On résume :
| f'(x) | - | 0 | + |
④ On calcule les valeurs des images des valeurs particulières.
f(-5)=3(-5)^2+12(-5)-5=10
f(-2)=3(-2)^2+12(-2)-5=-17
f(2)=3(2)^2+12(2)-5=31
⑤ On construit les flèches associées aux signes de la dérivées.
⑥ On obtient :
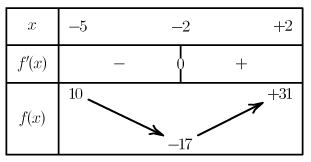
FD05 – Applications à l’étude des variations d’une fonction
Soit f une fonction dérivable sur un intervalle I :
Si f'(x)>0 alors la fonction est croissante sur I.
Si f'(x)=0 alors la fonction est constante sur I.
Si f'(x)<0 alors la fonction est décroissante sur I.
Si f(x)=2x alors f'(x)=2 or f'(x)>0 donc f est croissante.
Si f(x)=-3x alors f'(x)=-3 or f'(x)<0 donc f est décroissante.
SI pour une valeur x_0 appartenant à l’intervalle I, f'(x_0) s’annule en changeant de signe alors la fonction f passe par un extremum (minimum ou maximum) pour x=x_0.
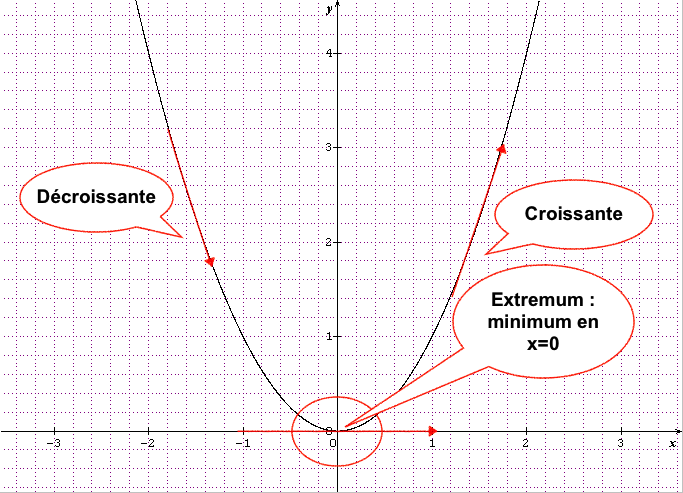
f'(x)=2x
Si x<0 alors f'(x)<0 donc la fonction est décroissante.
Si x=0 alors f'(x)=0 donc la fonction est constante.
Si x>0 alors f'(x)>0 donc la fonction est croissante.
La fonction f(x)=x^2 s’annule en x_0=0 en changeant de signe donc x_0=0 est un extremum ici un minimum.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
A l’aide du calcul de la dérivée, déterminer un extremum.
A l’aide du calcul de la dérivée, déterminer un extremum.
FD04 – QCM Dérivées
Cliquer sur le bouton « Départ » pour commencer le QCM
QCM Dérivées
Félicitation - vous avez complété QCM Dérivées.
Vous avez obtenu %%SCORE%% sur %%TOTAL%%.
Votre performance a été évaluée à %%RATING%%
FD03B – Exercices calcul de dérivées
f(x)=3x+2-\dfrac{2}{x}
f'(x)=3+\dfrac{2}{x^2} -> règle f+g
f(x)=-x^2+7x-10
f'(x)=-2x+7 -> règle f+g
f(x)=4x+8\sqrt{x}
f'(x)=4+\dfrac{4}{\sqrt{x}} -> règle f+g
FD-03A : Exercices calcul de dérivées
FD02 – Calcul de dérivées
Étant donnée une fonction f dérivable sur un intervalle I, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction f en x est appelée fonction dérivée de la fonction f sur I et est notée f'.
I=\mathbb{R} représente l’ensemble des réels et I=\mathbb{R}^+ représente l’ensemble des réels positifs.
| Fonction | Expression | Fonction dérivée |
| Constante | a | 0 |
| Affine | ax+b | a |
| Carrée | x^2 | 2x |
| Cube | x^3 | 3x^2 |
| Inverse | \dfrac{1}{x} | -\dfrac{1}{x^2} |
| Racine carrée | \sqrt{x} | \dfrac{1}{2\sqrt{x}} |
Si f(x)=2x alors f'(x)=2 => Fonction linéaire
Si f(x)=2x+4 alors f'(x)=2 => Fonction affine (=fonction linéaire + fonction constante)
Si f(x)=x^2 alors f'(x)=2x => Fonction carrée
Si f(x)=x^3 alors f'(x)=3x^2 => Fonction cube
Si f(x)=\dfrac{1}{x} alors f'(x)=-\dfrac{1}{x^2} => Fonction inverse
Si f(x)=\sqrt{x} alors f'(x)=\dfrac{1}{2\sqrt{x}} => Fonction racine carrée
Étant donnée deux fonctions f et h dérivables sur un intervalle I et un réel k telles que h=k \times f et , la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction h en x est appelée fonction dérivée de la fonction h sur I et est notée h' et est égale à k \times f'.
On en déduit que h'(x)=k \times f'(x)=2 \times 1=2.
On en déduit que h'(x)=k \times f'(x)=3 \times 2x=6x.
On en déduit que h'(x)=k \times f'(x)=5 \times \dfrac{1}{2\sqrt{x}}=\dfrac{5}{2\sqrt{x}}.
Étant donnée trois fonctions f,g et h dérivables sur un intervalle I et telles que h=f+g, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction h en x est appelée fonction dérivée de la fonction h sur I et est notée h' et est égale à f'+g'.
or f'(x)=2 et g'(x)=0. On en déduit que h'(x)=f'(x)+g'(x)=2+0=2.
or f'(x)=3x^2 et g'(x)=2x. On en déduit que h'(x)=f'(x)+g'(x)=3x^2+2x.
or f'(x)=\dfrac{1}{2\sqrt{x}} et g'(x)=2. On en déduit que h'(x)=f'(x)+g'(x)=\dfrac{1}{2\sqrt{x}}+2.
h(x)=2x^3-x^2+3x-2 donne h'(x)=6x^2-2x+3
FD01 : Approche de la dérivée
– à partir de son expression algébrique
f(x)=2x^3+2
– sa représentation graphique :
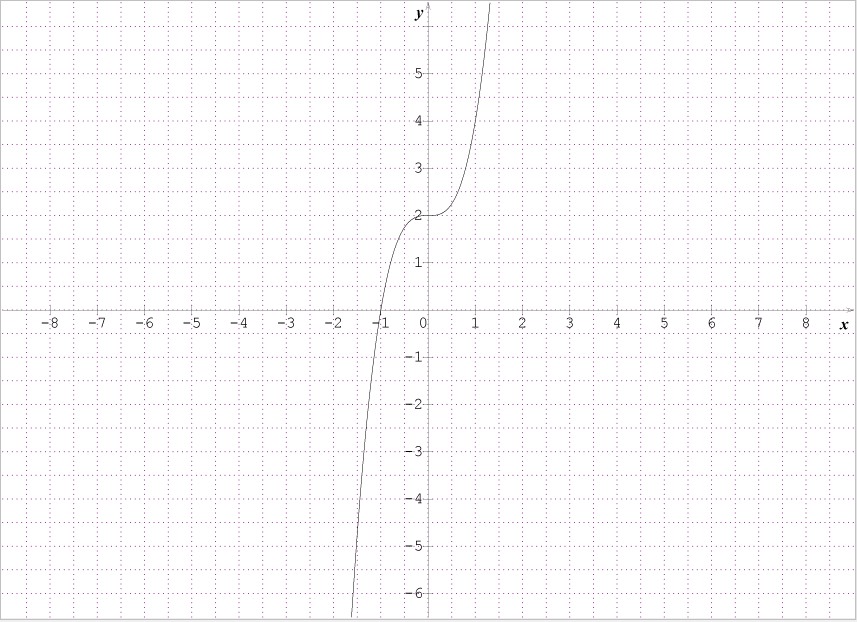
– et son tableau de valeurs :
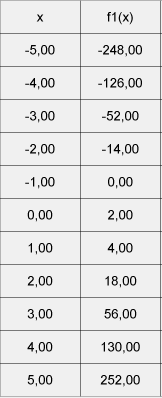
Prenons ce rugbyman qui tape dans un ballon :

Plusieurs trajectoires sont possibles :

La trajectoire peut être modélisée par une fonction numérique. Cette année, nous allons pouvoir prévoir les variations de la fonction numérique (ici la trajectoire).
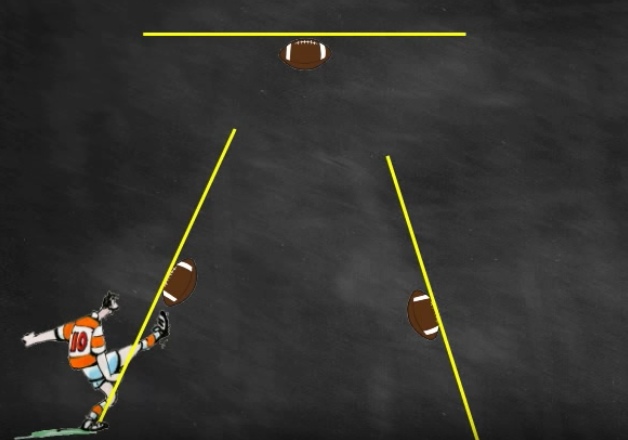
On va s’aider des tangentes en plusieurs points à la trajectoire du ballon.
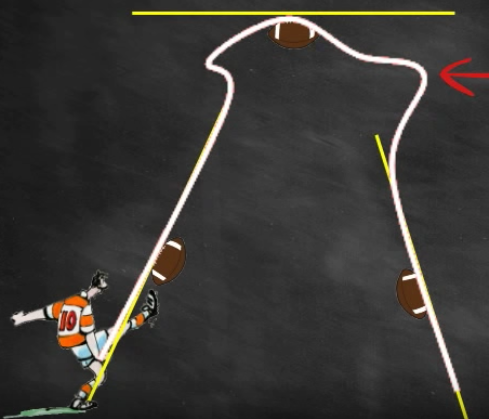
Pour être plus précis, on va multiplier les points de la trjectoire…

et calculer les tangentes.
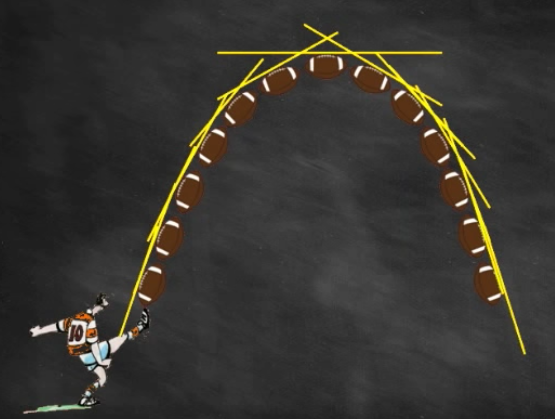
On a donc réussi à affiner la trajectoire du ballon.
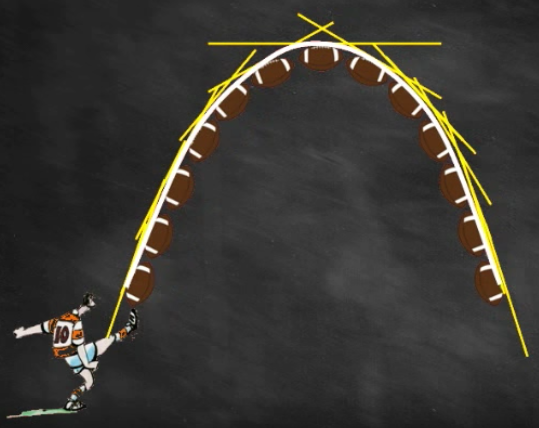
Les tangentes sont intéressantes car ce sont des droites donc faciles à étudier en mathématiques.
Les droites,représentations graphiques, ont été étudiées en seconde par leur fonction, la fonction affine f(x)=ax+b.
Une droite se caractérise avant tout par son coefficient directeur a qui nous indique si la droite est croissante ou décroissante.
Revenons une dernière fois sur notre rugbyman :
On voit que les tangentes ont un coefficient directeur positif quand la trajectoire monte et qu’elles ont un coefficient directeur négatif quand la trajectoire descend.
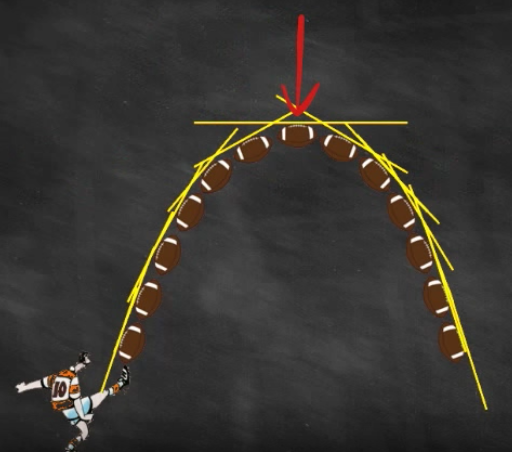
De plus lorsqu’on arrive au sommet de la trajectoire, le coefficient directeur de la tangente parallèle au sol (axe des abscisses) est nul.
– signe positif : trajectoire croissante
– signe nul : trajectoire constante
– signe négatif : trajectoire décroissante
C’est ce coefficient directeur de tangente que l’on appellera maintenant le nombre dérivé.
Il y autant de nombres dérivées que de tangentes possibles en chaque point de la courbe.
L’ensemble des nombres dérivés sont obtenus grâce à la fonction dérivée de la fonction numérique étudiée.
x \mapsto f'(x)
On dit « f prime de x ».
SG-10 – Salle de concert
Elle demande 3570€ la première journée et facture chaque journée supplémentaire 15% de moins que la précédente.
Jerry est manager de groupes musicaux et souhaite louer la salle pour des festivals.
On fixe u_n la suite représentant le coût des journées.
Une réduction de 15% correspond à un facteur multiplicateur de 100\%-15\%=85\%=\dfrac{85}{100}=0,85.
u_2=3570 \times 0,85=3034,50
La seconde journée coutera donc 3034,50€.
u_2=3034,50 \times 0,85=2579,325
La seconde journée coutera donc 2579,325€.
\dfrac{u_2}{u_1}=\dfrac{u_3}{u_2}=q
La suite u_n est une suite géométrique de raison q=0,85.
u_n=3570 \times 0,85^{n-1}
u_7=3570 \times 0,85^{6}
u_7=1346,42377078125
u_31=3570 \times 0,85^{30}
u_31=27,24
S=3570 \times \dfrac{0,85^{4}}{0,85-1}
S=11376,2513
S=3570 \times \dfrac{0,85^{7}}{0,85-1}
S=16170,2653
SG09 – Acheter ou louer
L’agence les informe que la propriétaire serait également disposée à leur vendre le bien pour 190 000 € (frais d’agence inclus). Envisageant de rester une vingtaine d’années dans cet appartement, le couple se demande s’il ne serait pas préférable d’acheter plutôt que de louer.
Jacques et Faty souhaitent connaître le montant total des loyers qu’ils auront à verser en 20 ans de location.
– Pour cela il faut déterminer le montant annuel des loyers qui sera le premier terme de la suite géométrique de raison q = 1,03 (augmentation de 3%).
– Ensuite il faut calculer la somme des 20 premiers termes de cette suite.
– On vérifie à l’aide d’un tableur ou de la calculatrice.
2. Mettre en œuvre votre méthode de résolution.
Annuellement, Jacques et Faty vont payer 8640€.
Une augmentation de 3% est égale à un facteur multiplicateur 100%+3%=103%=1,03.
Raison de la suite : q=1,03
Le prix du loyer sera la deuxième année de 8899,20€.
u_n=8640 \times 1,03^n-1
u_10=8640 \times 1,03^10-1
u_10=8640 \times 1,03^9
u_10=11273,24
Premier terme : u_1=8640
Raison : q=1,03
Sommes des termes :
S=u_1 \times \frac{q^n-1}{q-1}=8640 \times \frac{1,03^{20}-1}{1,03-1}
S=232160,04
Faty et Jacques ont donc plutôt intérêt à acheter l’appartement.
SG08 – Interrogation
| \Box | u_{n}=u_{1} \times q^n | \Box | u_{n}=u_{0} \times q^n |
| \Box | u_{n}=u_{0} \times q^{n-1} | \Box | u_{n}=u_{1} \times q^{n-1} |
1-t%=1-7%=1-0,07=0,93
1+t%=1+4%=1+0,04=1,04
| \Box | S=u_0 \times \dfrac{q^{n+1}-1}{q-1} | \Box | S=u_1 \times \dfrac{q^{n-1}-1}{q-1} |
| \Box | S=u_0 \times \dfrac{q^{n}-1}{q-1} | \Box | S=u_1 \times \dfrac{q^{n}-1}{q-1} |
(u_{n}) est une suite géométrique de raison q
u_{n}=200 \times {1,1}^n
u_{3}=200 \times {1,1}^3
u_{3}=266,2
u_{n}=800 \times {0,87}^{n-1}
u_{6}=800 \times {0,87}^{6-1}
u_{6}=800 \times {0,87}^5
u_{6}=398,74
S=400 \times \dfrac{1,78^{7+1}-1}{1,78-1}
S=400 \times \dfrac{1,78^{8}-1}{1,78-1}
S=51167,52
S=1000 \times \dfrac{0,81^{10}-1}{0,81-1}
S=4623,28
1+t%=1+7%=1+0,07=1,07=q
u_0=1000
La production va suivre les valeurs d’une suite géométrique de premier terme u_0=1000 et de raison q=1,07
Le rang 0 correspond à l’année 2017.
L’année 2024 correspond donc au rang 7. ( si vous prenez u_1=1000 alors le rang sera 8)
On nous demande ici le nombre de pièces prévues et non la somme des pièces vendues depuis le début…on applique alors :
u_{n}=u_{0} \times q^n
u_{n}=1000 \times {1,07}^n
u_{7}=1000 \times {1,07}^7
u_{7}=1000 \times {1,07}^7
u_{7}=1605,78
L’entreprise aura une production de 1605 pièces en 2024.
SG07 – QCM : Somme des n premiers termes d’une suite géométrique
Cliquer sur le bouton « Départ » pour commencer le QCM
QCM Calcul des n premiers termes d'une suite géométriques
Félicitation - vous avez complété QCM Calcul des n premiers termes d'une suite géométriques.
Vous avez obtenu %%SCORE%% sur %%TOTAL%%.
Votre performance a été évaluée à %%RATING%%
SG06 : Somme des n premiers termes d’une suite géométrique
Pour calculer la somme des n termes d’une suite arithmétique, il faut :
- Déterminer le nombre de termes de la suite.
- Connaître le premier terme u_0 ou u_1 et la raison.
Appliquer l’une des formules suivantes en fonction du premier terme u_0 :
ou u_1 :
Exercices d’application de la formule :
S=2 \times\dfrac{3^{6+1}-1}{3-1}=2 \times\dfrac{2187-1}{3-1}=2 \times 1093= 2186
S=3 \times\dfrac{2^{5}-1}{2-1}=3 \times\dfrac{32-1}{2-1}=3 \times 31= 93
S=128 \times\dfrac{(\dfrac{1}{2})^{5}-1}{\dfrac{1}{2}-1}
S=128 \times\dfrac{0,03125-1}{-0,5}=128 \times 1,9375= 248
SG05 : Watt
1-t%=1-6%=1-0,06=0,94
On multiplie donc par 0,94 la production de janvier pour connaître celle de février.
P_2=P_1 \times 0,94=10000 \times 0,94=9400
P_3=P_2 \times 0,94=9400 \times 0,94=8836
P_n=P_1 \times q^{n-1}
enfin
P_n=10000 \times (0,94)^{n-1}
On applique la formule P_n=10000 \times (0,94)^{n-1} avec n=12.
P_{12}=10000 \times (0,94)^{12-1}
enfin
P_{12}=10000 \times (0,94)^{11}=4759
La production en décembre 2017 sera de 4759 ampoules.
S=P_1 \times \dfrac{1-q^{n}}{1-q}
S=10000 \times \dfrac{1-(0,94)^{n}}{1-0,94}
enfin pour les 12 premiers mois qui forme l’année
S=10000 \times \dfrac{1-(0,94)^{12}}{1-0,94}=87246,61
La production pour l’année 2017 sera de 87 246 ampoules.
SG04 – Problème et somme
Définition : Une annuité est une somme d’argent versée annuellement par un emprunteur pour rembourser une dette. Elle est constituée d’une partie du capital emprunté, ainsi que des intérêts dus. Elle peut être variable ou constante d’une année à l’autre.
A. Calcul des annuités
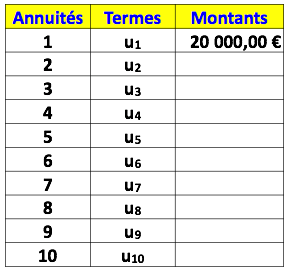
Soit u_1, u_2, …, u_{10} les montants des dix annuités.
u_2=20000 \times 1,05
u_2=21000
u_3=21000 \times 1,05
u_3=22050
u_4=22050 \times 1,05
u_4=23152,5
u_{n}=20000 \times 1,05^{n-1}
u_{10}=20000 \times 1,05^{10-1}
u_{10}=20000 \times 1,05^{9}
u_{10}=31026,56
Dans 10 ans, l’annuité sera alors de 31026,56 €.
B. Montant total du remboursement
Sur une feuille de calcul d’un tableur, reproduire la tableau représenté ci-dessus. Pour cela, saisir :
C3=C2 \times 1.05
L’entreprise aura alors remboursée 251558 € de son emprunt au bout de 10 ans.
On verra juste après qu’une formule existe pour calculer n’importe quelle somme de n termes pour une suite géométrique.
SG03 – Cours sur les suites géométriques
Définition
Exemple :
Notation
Exemple :
On utilisera les notations suivantes :
Pour le terme précédent de le n-ième terme : u_{n-1}
Pour le terme suivant de le n-ième terme : u_{n+1}
Définition
u_n=u_{n-1} \times q
Définition
u_{n+1}=u_{n} \times q
Exemple :
Définition :
u_{n}=u_{0} \times q^n
ou
u_{n}=u_{1} \times q^{n-1}
Entraînement :
https://www.thatquiz.org/fr-2/?-j100h-l2-mpnv600-p0
Exemple :
Exercices :
Calculer u_1 et fonction de u_2.
Calculer u_n en fonction de n.
Calculer u_5.
Calculer u_2 et fonction de u_3.
Calculer u_n en fonction de n.
Calculer u_5.
Calculer u_2 et fonction de u_3.
Calculer u_n en fonction de n.
Calculer u_5.
En déduire q.
Calculer ensuite u_1
Calculer u_n en fonction de n.
Calculer u_6.
En déduire q.
Calculer ensuite u_1
Calculer u_n en fonction de n.
Calculer u_8.