Parmi ceux venant en voiture, 8 viennent seuls et les autres font du covoiturage.
L’entreprise compte 43 salariés.
L’évènement A correspond à « L’employé vient en transport collectif.(bus et covoiturage) »
Déterminer p(A). Arrondir au centième.
p(A)=\dfrac{14+14}{43}=0,65
La probabilité p(A) est de 0,65.
Déterminer p(B). Arrondir au centième.
p(B)=\dfrac{22}{43}=0,51
La probabilité p(B) est de 0,51.
L’évènement concerne les salariés venant au travail en voiture collectivement, soit en covoiturage.
La probabilité est de 0,33.
Proba13 – Baccalauréat
On considère un établissement scolaire de 2000 élèves, regroupant des collégiens et des lycéens.
– 19 % de l’effectif total est en classe de terminale;
– parmi ces élèves de terminale, 55% sont des filles;
– le taux de réussite au baccalauréat dans cet établissement scolaire est de 85%;
– parmi les candidates ayant échoué, la proportion des filles a été de \dfrac{8}{19}.
| Elèves | Garçons | Filles | Total |
|---|---|---|---|
| Réussite | 124 | 23 | 14 |
| Echec | |||
| Total |
Après la publication des résultats, on choisit au hasard un élève parmi l’ensemble des élèves de terminale. On considère les évènements suivants :
– G : « l’élève est un garçon »
– R : « l’élève a eu son baccalauréat »
Dans la suite, on donnera les résultats sous forme décimale, arrondis à 10^{-2} près.
2. Définir les évènements suivants par une phrase :
3. Calculer les probabilités des évènements suivants :
4. On choisit un élève au hasard parmi les bacheliers.
Proba12 – Exercice maison – Prince charmant
Exercice 2
Un prince charmant se doit de partir à l’aventure et d’affronter des périls. Dans 42% des cas, il affronte un Dragon, dans 30% ce sont des Trolls et dans les autres cas, c’est le Chevalier Noir.
Dans tous les cas, il réussit sa quête avec une probabilité de 0,8.
Tuer un Dragon lui rapporte 1000 pièces d’or, un Troll 500 et le Chevalier Noir 300.
1.a. Construire l’arbre correspondant. On appellera D l’évènement Dragon, T l’évènement Troll et C l’évènement Chevalier Noir et enfin Q est l’évènement quête réussie.
1.b. Décrire \overline{Q} à l’aide d’une phrase.
2. Un prince part à l’aventure. Quelle est la probabilité :
a. qu’il gagne 1000 pièces d’or ?
b. qu’il gagne des pièces d’or ?
c. qu’il revienne bredouille ?
3. Recopier et compléter le tableau suivant :
| Gains en pièces d’or | 1000 | 500 | 300 | 0 |
|---|---|---|---|---|
| Probabilité |
Proba11 – Exercice maison – Arbre et probabilités
Exercice 1
On lance deux fois de suite une pièce de monnaie. Il s’agit d’une expérience aléatoire à deux épreuves.
Soit E l’évènement : « On obtient au moins une fois la face PILE. »
Calculer P(E) en réalisant l’arbre correspondant.
Exercice 2
Lisa a dans un tiroir trois paires de chaussettes de type identique mais de couleurs différentes : noire, rouge et beige. Dans l’obscurité, elle prend au hasard deux chaussettes parmi les six.
Proba8 : Calculs de probabilités avec union et intersection
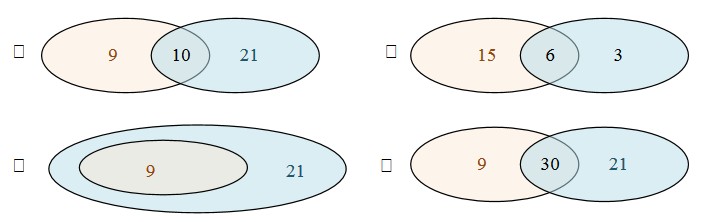
Attention, certains élèves ne sont ni majeurs ni titulaires d’un CAP.
– le diagramme 2 ne compte que 24 élèves en tout.
– le diagramme 3 ne compte que 21 élèves en tout.
– dans le diagramme 4, tous les élèves sont majeurs et ont un CAP.
\Box \quad p(A \cup B) \quad \Box \quad p(A - B) \quad \Box \quad p(A \cap B)
\Box \quad p(A \cup B) \quad \Box \quad p(A + B) \quad \Box \quad p(A \cap B)
p(A \cup B)=p(A)+p(B)-p(A \cap B)
p(A \cup B)=0,7+0.3-0.33=0.67
Proba9 : Exercices en ligne
Liste d’exercices en ligne
Proba7 : Exercice d’arbre
Ω={JJ,JV,JB,VJ,VV,VB,BJ,BV,BB}.
Proba1 – Vocabulaire des probabilités
Définition
Exemple :
– on peut déterminer toutes les issues possibles : ici on peut obtenir un 7, un 8 , un 9, un 10, un valet, une dame, un roi ou un as.
– on ne sait pas laquelle de ces issues va se réaliser.
Définition
Exemples :
Dans un jeu de 32 cartes, l’expérience « tirer une carte au hasard sans tenir compte de sa couleur », a pour univers l’ensemble des issues suivantes : Ω = {7; 8; 9; 10; valet; dame; roi; as}.
Propriétés
Proba2. Calculer une probabilité
Enoncé
Définition
p(A)=\dfrac{3}{8}= 0,375
Définition
Exemple :
p(\overline{A})=\dfrac{5}{8}= 0,625
Proba3. Probabilité d’un évènement et fréquences des échantillons
Définition
Exemple :
A. SIMULATION
p(A)=\dfrac{128}{365}= 0,35
Dans la colonne A, saisir les jours de 1 à 365.
Dans la colonne B, afficher 1 pour un jour de pluie et 0 pour un jour sans pluie. Quelle est la formule permettant de faire la simulation d’un jour de pluie ?
Dans la colonne C, afficher le cumul des nombres de jours de pluie :
C1:=B1 ; C2:=C1+B2 ; puis copier C2 jusqu’en C365.
Dans la colonne D, afficher la fréquence des jours de pluie :
D1:=C1/A1, puis recopier jusqu’en D365
Sélectionner la colonne D puis insérer un graphique de forme « nuage de points ». Appuyer F9 pour réaliser plusieurs simulations.
Le nuages de points obtenu ressemble à celui-ci.
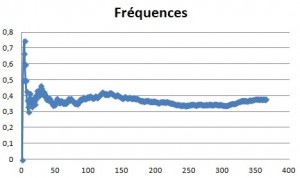
B. INTERPRETATIONS
| Durées | Semaine (7 jours) | Quinzaine (15 jours) | Mois (30 jours) | Trimestre (90 jours) | Semestre (180 jours) | Année (365 jours) |
| Fréquence (selon simulation) | …….. | …….. | …….. | …….. | …….. | …….. |
Les résultats dépendent de vos simulations, voici un exemple :
| Fréquence | 0,43 | 0,36 | 0,40 | 0,39 | 0,37 | 0,35 |
Proba4. Probabilités lors de choix successifs
Définition
– n possibilités pour le 1er choix,
– (n – 1) possibilités pour le 2nd choix,
– (n – 2) possibilités pour le 3e, etc.
Exemple :
Soit A l’évènement « obtenir deux couleurs différentes ».
Nb d’issues possibles : 32
p(A)=\dfrac{4}{32}= 0,125
Nb d’issues possibles : 31
p(A)=\dfrac{3}{31}= 0,097
Proba5. Simuler un tirage avec un arbre des évènements
Définition
A chaque étape il faut notifier une issue possible par une ramification.
La somme des probabilités de chaque étape est égale à 1.
Exemple
On réalise deux tirages successifs avec remise.
Voici l’arbre des évènements représentant cette expérience.
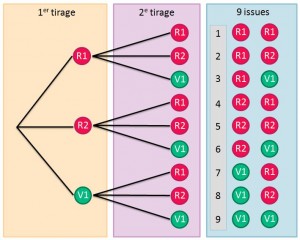
Application
On réalise trois tirages successifs sans remise.
Sinon il reste toujours 3 possibilités car il existe encore des boules des trois couleurs.
Soit l’évènement A « Obtenir trois boules de couleurs différentes ».
Soit l’évènement B « Obtenir au moins deux boules de couleurs identiques ».
Proba6. Opérations sur les probabilités
Définition
=> L’intersection des événements, notée A ∩ B, est l’ensemble des résultats qui réalisent à la fois les deux événements A et B.
=> La réunion des événements, notée A ∪ B, est l’ensemble des résultats qui réalisent l’un ou l’autre des événements A et B.
=> La probabilité de la réunion des événements A et B se calcule par la relation :
p(A∪B) = p(A) + p(B) – p(A∩B).
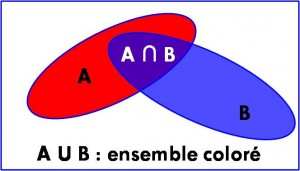
Exemple :
Sur 20 filles 12 participent dans une équipe, sur 10 garçons il n’y a que 40% qui participent ans un équipe.
| Elèves | Joueurs | Spectateurs | TOTAL |
| Garçons | …….. | …….. | …….. |
| Filles | …….. | …….. | …….. |
| TOTAL | …….. | …….. | …….. |
| Elèves | Joueurs | Spectateurs | TOTAL |
| Garçons | 4 | 6 | 10 |
| Filles | 12 | 8 | 20 |
| TOTAL | 16 | 14 | 30 |
\quad \Box A U B \quad \Box A ∩ B \quad \Box A x B
\quad \Box A U B \quad \Box A x B \quad \Box A ∩ B
p(D) = p(A) + p(B) – p(C) = 0,67 + 0,53 – 0,40 = 0,80
Autre Méthode :
Le nombre d’élèves concernés par l’évènement D est : 20 filles + 4 garçons joueurs = 24 élèves
p(D)=\dfrac{24}{30}= 0,80
Proba10. CCF exemple 1 : « Menu formule »
Enoncé
– 3 entrées : œuf mimosa à 2 € – salade niçoise à 4 € – charcuterie à 7 €
– 2 plats du jour : steak frites à 10 € – saumon riz à 12 €
– 2 desserts : tarte aux pommes à 6 € – gâteau aux amandes à 8 €

œuf mimosa + steak frites + tarte aux pommes
Tarif du menu choisi : 2 + 10 + 6 = 18 €
CCF 1. tableur2 augmentation tarif
Il faut faire baisser le tarif des charcuteries à 6 € pour obtenir 4 menus à 22 €.
Enoncé
| Prix en € | [17 ; 19[ | [19 ; 21[ | [21 ; 23[ | [23 ; 25[ | [25 ; 27[ |
| Effectif | 97 | 313 | 391 | 292 | 107 |
f=\dfrac{\text{nb cas favorables}}{\text{nb total de possibilités}} x 100
| Prix en € | [17 ; 19[ | [19 ; 21[ | [21 ; 23[ | [23 ; 25[ | [25 ; 27[ |
|---|---|---|---|---|---|
| Effectif | 97 | 313 | 391 | 292 | 107 |
| Fréquence en % | 8,08 | 26,08 | 32,58 | 24,33 | 8,92 |
Événement A : « le montant de la note est égal ou supérieur à 21 € »
Événement B : « le montant de la note est inférieur à 23 € »
p(A)=\dfrac{\text{nb d'issues favorables}}{\text{nb total d'issues possibles}}
p(A)=\dfrac{790}{1200}= 0,66
p(B)=\dfrac{801}{1200}= 0,67
ou bien
(A U B) : « le montant de la note est compris entre 17 € et 27 €, non inclus pour ce dernier tarif »
p( A U B) = 1
p(A U B) = p(A) + p(B) – p(A ∩ B)
ou bien
(A ∩ B) : « le montant de la note est compris entre 21 € et 23 €, non inclus pour ce dernier tarif »
| Prix en € | [17 ; 19[ | [19 ; 21[ | [21 ; 23[ | [23 ; 25[ | [25 ; 27[ |
|---|---|---|---|---|---|
| Effectif | 1 | 3 | 4 | 3 | 1 |
| Fréquence en % | 8,08 | 25,00 | 33,33 | 25,00 | 8,08 |